I problemi per il millennio

Millennium problems

Se sei un vero appassionato della matematica, probabilmente avrai sentito parlare dei problemi per il millennio. Altrimenti, sei nel post giusto! Abbiamo già discusso dell'utilità della matematica nel primo post di questo blog. Il 24 maggio 2000 Clay Mathematics Institute (CMI) ha deciso di presentare al convegno del Millennio di Parigi sette problemi della matematica allora irrisolti e di cui finora soltanto uno è stato risolto. La risoluzione dei problemi porterebbe a conseguenze estremamente pratiche in campi che spaziano dall'economia alla tecnologia. Per ogni problema risolto l'istituto assegnerà un milione di dollari. Vediamo quali sono questi problemi.

Sommario

• Teoria di Yang-Mills e il gap di massa
• Ipotesi di Riemann
• P vs NP
• Le equazioni di Navier-Stokes
• Congettura di Hodge
• Congettura di Poincaré
• Congettura di Birch e Swinnerton-Dyer
• Riferimenti
• Fonte delle immagini

Teoria di Yang-Mills e il gap di massa

Status: non risolto

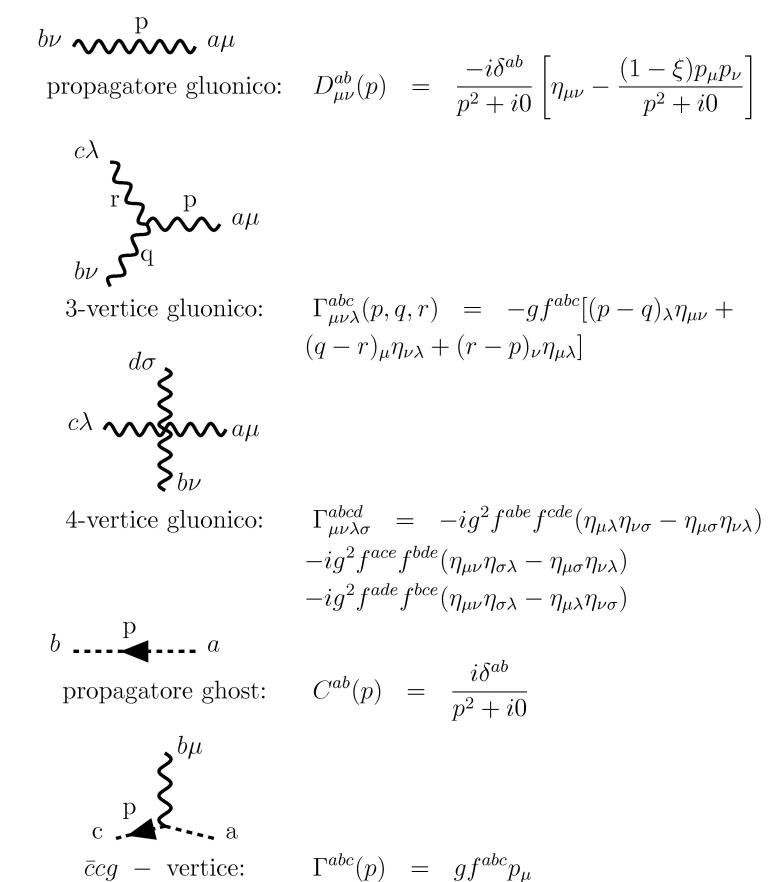Figura 1: le regole di Feynman.

Hai presente quando il regista del film non è in grado di spiegare una nuova tecnologia e la giustifica con "meccanica quantistica"? La fisica viene rigorosamente suddivisa in classica e quantistica. Con il termine "fisica classica" s'intendono tutte le leggi che sono state formulate prima del XX secolo, con particolare attenzione ai principi della dinamica newtoniani. Questi principi descrivono molto bene il moto dei corpi nello spazio-tempo per velocità lontane da quella della luce. Nel mondo microscopico, in cui le particelle si muovono prossime alla velocità della luce, le leggi di Newton non sono valide e alla fine del XIX secolo si rese necessaria fondare una nuova teoria: la meccanica quantistica. 

Nel 1954 i fisici Chen Ning Yang e Robert Mills formularono una teoria di gauge fondata sul gruppo \(SU(n)\) per descrivere il comportamento delle particelle elementari, diventando un fondamento della meccanica quantistica. Nonostante le previsioni della teoria siano state testate in molti laboratori, la teoria ha un fondamento matematico che non risulta ancora chiaro. Il successo della teoria di Yang e Mills si basa su una proprietà che viene chiamata gap di massa. Le particelle, pur viaggiando a velocità luminare, possiedono una massa positiva. Ciò è stato verificato grazie a esperimenti e simulazioni al computer, ma non si comprende come sia possibile da un punto di vista teorico.

Secondo il CMI [1] (tradotto dall'inglese):

I progressi nello stabilire l'esistenza della teoria di Yang-Mills e un divario di massa richiederanno l'introduzione di nuove idee fondamentali sia in fisica che in matematica

Ipotesi di Riemann

Status: non risolto

Figura 2: valore assoluto della funzione \(\zeta\) di Riemann sul piano complesso. La funzione assume un valore minore nelle zone a maggior tonalità di blu.

Abbiamo già parlato dell'ipotesi di Riemann in un post precedente. Questa è una congettura del matematico tedesco Bernhard Riemann formulata nel XIX secolo secondo cui la distribuzione dei numeri primi è strettamente legata agli zeri della cosiddetta funzione zeta di Riemann:

$$ \zeta (s) = \sum\limits_{n=1}^\infty \dfrac{1}{n^s},\mspace{5mu} s\in \mathbb{C} $$

che nasce dal prolungamento analitico della serie di Dirichlet. 

In particolare, l'ipotesi di Riemann afferma che tutte le soluzioni non banali della funzione zeta si trovano su una certa retta verticale del piano di Argand-Gauss. Poiché \(\zeta\) può essere espressa in funzione dei numeri primi come

\( \quad \zeta (x) = \prod\limits_{p \text{ primo}}^\infty \dfrac{1}{1-p^{-x}},\mspace{5mu} x\in \mathbb{R} \)

si comprende come gli zeri della funzione \(\zeta\) diano informazioni sulla distribuzione dei numeri primi sulla retta reale. 

L'ipotesi è stata verificata per le prime 10.000.000.000.000 soluzioni [2], ma una sua dimostrazione rigorosa resta tuttora vacante. Se l'ipotesi venisse verificata, ciò avrebbe profonde conseguenze nella sicurezza telematica, la quale fa largo uso dei numeri primi.

P vs NP

Status: non risolto

Figura 3: modello di macchina di Turing.

Il problema delle classi P e NP è un profondo quesito della teoria della complessità computazionale. Questo problema fu indipendentemente formulato nel 1971 da Stephen Cook e Leonid Levin e chiede di rispondere alla domanda

P è uguale a NP?

Con "P" si intende la classe dei problemi decisionali la cui risoluzione avviene in un tempo polinomiale rispetto alla dimensione dei dati di input con una macchina di Turing deterministica. "NP", invece, indica la classe di problemi che possono essere risolti in un tempo polinomiale con una macchina di Turing non deterministica. 

Brevemente, ogni problema per cui un computer è in grado di verificare se un valore sia una soluzione in un tempo accettabile è anche un problema che il computer è in grado di risolvere in un tempo accettabile?

Le equazioni di Navier-Stokes

Status: non risolto

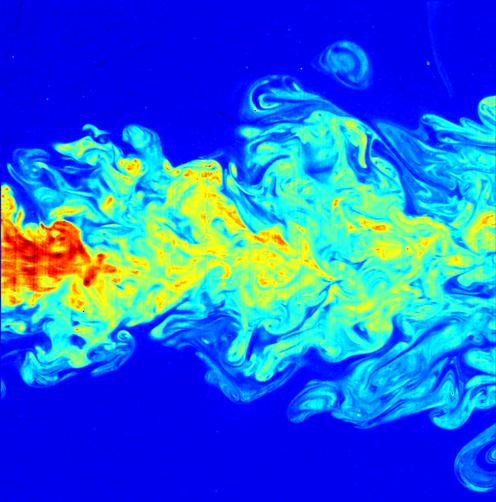Figura 4: flusso turbolento di un fluido. Fluorescenza indotta da laser.

La nostra comprensione del moto turbolento dei fluidi ci viene data per la maggior parte da modelli empirici e simulazioni al computer, nonostante questo sia un fenomeno comune della realtà quotidiana. Comprendere le leggi del moto turbolento di un fluido avrebbe profondi risvolti nei campi dell'ingegneria e della fisica.

Le equazioni di Navier-Stokes sono un sistema di tre equazioni alle derivate parziali che descrivono un fluido viscoso lineare. È stato possibile finora risolvere queste equazioni per casi particolari, ma il caso generale resta un problema irrisolto. 

Le equazioni riguardano:

• il principio di conservazione della massa, espresso come equazione di continuità:

$$ \dfrac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{\mathbf{u}}) = 0 $$

dove \(\rho\) è la densità di massa, \(t\) è il tempo e \(\vec{\mathbf{u}}\) è il campo di velocità del fluido.

• l'equazione di bilancio della quantità di moto:

$$ \dfrac{d}{dt} \int\limits_{V} \rho \vec{\mathbf{u}} dV + \oint\limits_{\partial V} (\rho \vec{\mathbf{u}}) \vec{\mathbf{u}} \cdot d\vec{\mathbf{S}} = \int\limits_{V} \vec{\mathbf{F}} dV + \oint\limits_{\partial V} \underline{\underline{T}} dS $$

dove \(\underline{\underline{T}}\) è il tensore degli sforzi nel fluido.

• l'equazione di conservazione dell'energia:

$$ \dfrac{\partial (\rho E)}{\partial t}+ \Phi_E = - P_p + P_S + P_c - \nabla \cdot \vec{\mathbf{q}} $$

dove \(E\) è l'energia totale per unità di massa, \(\Phi_E\) è il flusso netto di energia totale, \(P_p\), \(P_S\) e \(P_c\) sono le potenze di pressione, degli sforzi viscosi e delle forze di campo e \(\vec{\mathbf{q}}\) è il flusso termico.

Congettura di Hodge

Status: non risolto

Figura 5: superficie di Togliatti.

La topologia è la branca della matematica che si occupa di studiare le proprietà geometriche degli oggetti matematici. Nell'ultimo secolo i matematici sono riusciti a sviluppare potenti strumenti in grado di definire concetti come la misura di uno spazio in due o più dimensioni, riuscendo a indagare sulla forma di figure sempre più complicate. La tecnica si basa sull'approssimazione della forma di un oggetto "incollando" blocchi geometrici. Purtroppo, la tecnica si è rivelata tanto efficace che l'interpretazione geometrica di tali blocchi è diventata difficile o impossibile. 

La congettura del matematico britannico William Vallance Douglas Hodge sostiene che per un tipo di spazio, detto varietà algebrica proiettiva, i blocchi, chiamati cicli di Hodge, non sono altro che combinazioni lineari razionali di cicli algebrici.

Congettura di Poincaré

Status: risolto

Figura 6: superficie topologicamente omeomorfa a una 2-sfera.

Il matematico Henri Poincaré formulo nel 1904 la sua famosa congettura:

Ogni 3-varietà semplicemente connessa chiusa (ossia compatta e senza bordi) è omeomorfa a una sfera tridimensionale.

Cosa significa? S'immagini di legare a un pallone un elastico come in Figura 6. Sei in grado di deformare l'elastico fino a farlo coincidere in un solo punto senza staccare l'elastico dalla superficie del pallone. Per questo motivo, si dice che il pallone è una superficie topologicamente omeomorfa a una 2-sfera (nel linguaggio comune semplicemente "sfera"). Se provassimo ad avvolgere un elastico intorno a una ciambella in qualsiasi modo, non potremmo in ogni caso farlo ritrarre fino a un punto senza rompere l'elastico. Pertanto, la ciambella non è una superficie topologicamente omeomorfa a una 2-sfera. 

La congettura di Poincaré afferma che la 3-sfera è l'unica varietà tridimensionale su cui qualsiasi cammino chiuso (l'elastico della nostra analogia) può essere contratto fino a diventare un punto. La congettura era già stata dimostrata per i casi \(n\)-dimensionali con \(n \geq 4\) già nel 1982, ma nel 2000 il caso tridimensionale era ancora irrisolto. 

Una dimostrazione della congettura sarebbe stata utile alla comprensione delle possibili topologie della teoria delle stringe e di altre teorie della fisica quantistica. Nel 2003 il matematico russo Grigorij Jakovlevič Perel'man pubblico un articolo e nel 2004 le sue tecniche venivano considerate le migliori per affrontare la dimostrazione della congettura. La comunità scientifica riconobbe l'importanza di Perel'man nella risoluzione della congettura, ma il matematico rifiutò sia la Medaglia Fields, che il premio dell'istituto Clay [3].

Congettura di Birch e Swinnerton-Dyer

Status: non risolto

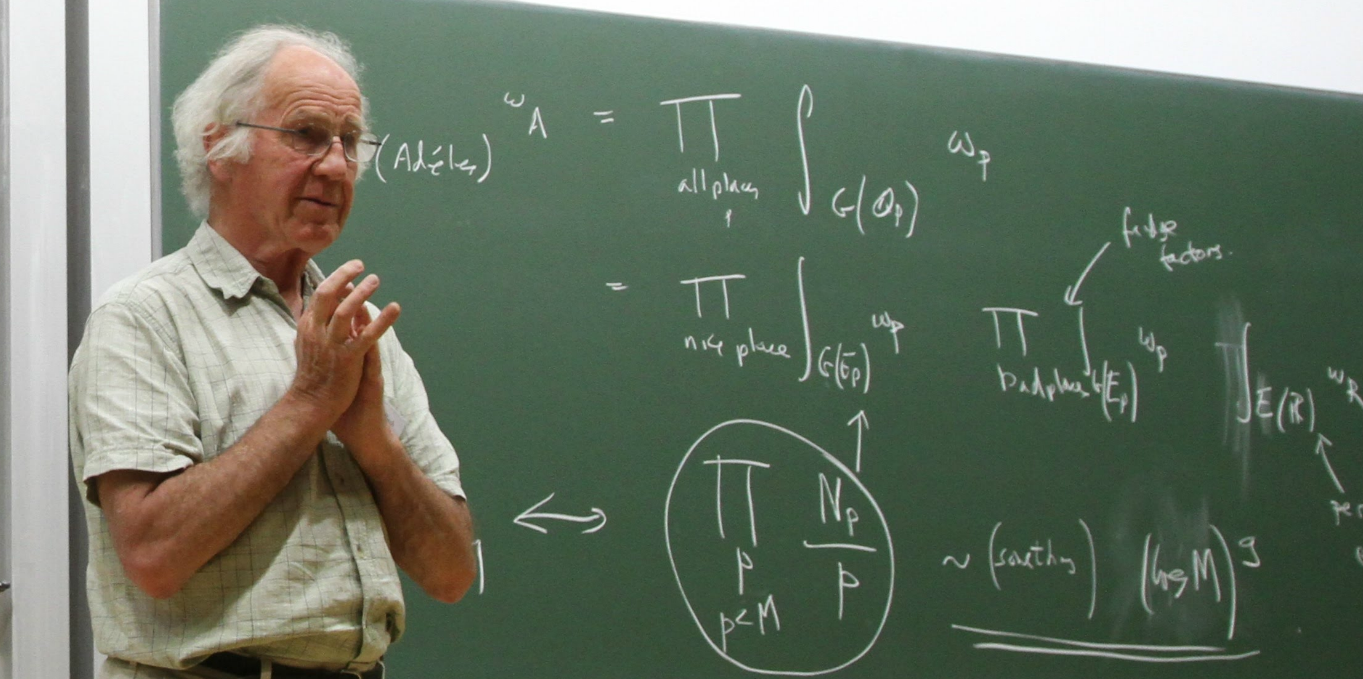Figura 7: Bryan Birch che spiega la congettura di Birch e Swinnerton-Dyer all'Università di Cambridge il 4 maggio 2011.

Si chiama equazione diofantea un'equazione a una o più incognite a coefficienti interi di cui si cercano le soluzioni intere. Un esempio è l'equazione

\( \quad x^2 - 2y^2 = 1 \)

Il decimo problema di Hilbert chiedeva l'esistenza o meno di un algoritmo che generalizzasse la risoluzione di un'equazione diofantea qualsiasi, algoritmo che nel 1970 Yuri Matiyasevich dimostrò essere inesistente. Tuttavia, se i punti di una varietà abeliana sono le soluzioni dell'equazione, la congettura di Birch e Swinnerton-Dyer afferma che la dimensione del gruppo di punti razionali è correlata al comportamento di una certa funzione zeta \(\zeta(s)\) associata in un intorno del punto \(s=1\). In particolare, se \(\zeta(1)=0\), allora esistono infiniti punti razionali soluzioni, mentre se \(\zeta(1) \neq 0\), allora esiste solo un numero finito di soluzioni.

Riferimenti

[1] Yang–Mills and Mass Gap | Clay Mathematics Institute

[2] Riemann Hypothesis | Clay Mathematics Institute

[3] Congettura di Poincaré - Wikipedia

Fonte delle immagini

Figura d'intestazione: Editor di immagini online gratis per graphic design - Pixlr.com

Figura 1: Di Marco Frasca - Autoprodotto, Pubblico dominio, https://commons.wikimedia.org/w/index.php?curid=5278383.

Figura 2: Nessun autore leggibile automaticamente. Conscious presunto (secondo quanto affermano i diritti d'autore). - Nessuna fonte leggibile automaticamente. Presunta opera propria (secondo quanto affermano i diritti d'autore). CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=939039.

Figura 3: Di Rocky Acosta - opera propria, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=24369879.

Figura 4: Di C. Fukushima and J. Westerweel, Technical University of Delft, The Netherlands - Opera propria, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=3082535.

Figura 5: Di Claudio Rocchini - Opera propria, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10773434.

Figura 6: Di Salix alba di Wikipedia in inglese, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=1972330.

Figura 7: Di William Stein - Stein, William Sage for Power Users, p. 108 . L'immagine a piena grandezza è disponibile su https://code.google.com/p/sage-power-book/source/browse/graphics/birch.png, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=26010832.